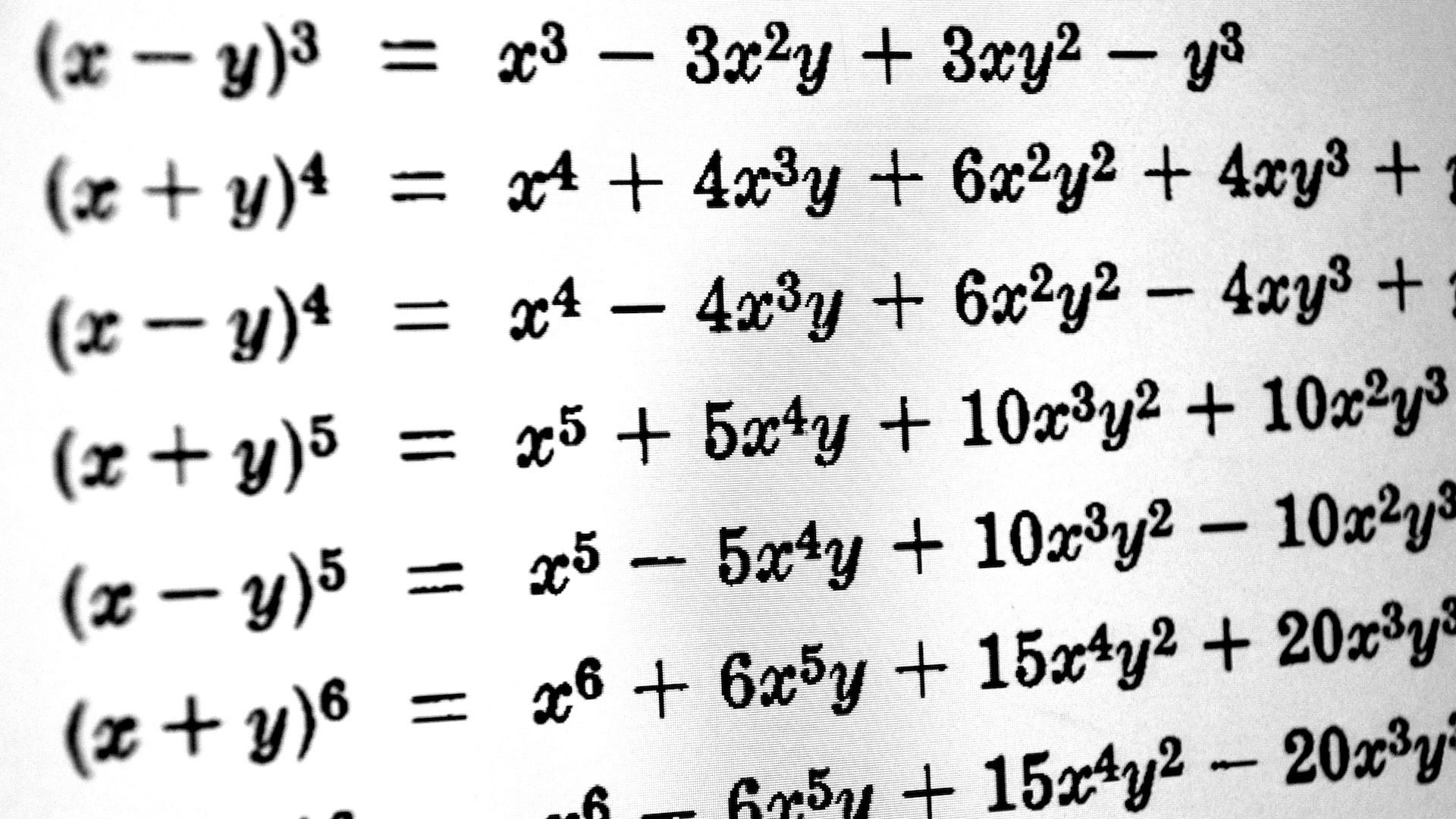
Polynomial equations form the backbone of contemporary science, offering a mathematical foundation for areas such as celestial mechanics, computer graphics, forecasts of market trends, and many others. However, despite most high school students being able to tackle basic polynomial equations, finding solutions for those with higher orders continues to evade even experienced mathematicians.
Currently, the mathematician from the University of New South Wales is Norman Wildberger And an independent computer scientist named Dean Rubine has discovered the initial comprehensive technique for tackling these highly challenging equations. They outlined their methodology on April 8 in the journal The American Mathematical Monthly .
A polynomial represents an algebraic expression where variables are elevated to a non-negative exponent, such as x² + 5x + 6 = 0. This concept belongs to one of the earliest ideas in mathematics, with origins dating back to ancient times in Egypt and Babylonia.
For many years, mathematicians have been able to solve basic polynomials with ease. Yet, dealing with high-order polynomials—those where \(x\) is elevated beyond the fourth power—has remained challenging. Typically, for solving second-, third-, and fourth-degree equations, one employs methods involving radical expressions—the roots of exponentials. But here’s the catch: these radicals frequently correspond to non-repeating infinite decimal sequences known as irrational numbers; think of them as unending strings of digits after the decimal point, much like pi .
Related: Mathematicians have recently resolved a century-old challenge, bringing together three physical theories.
Even though mathematicians can employ radicals to determine rough solutions for separate high-degree polynomials, they've had difficulty deriving a universal formula applicable to all such equations. This challenge exists due to the nature of irrational numbers, which cannot be completely resolved. As Wildberger pointed out, achieving this would require "an endless amount of effort and storage space bigger than the known universe." statement .
In their new method, Wildberger and his colleagues avoided radicals and irrational numbers entirely. Instead, they employed polynomial extensions known as power series. These are hypothetically infinite strings of terms with the powers of x, commonly used to solve geometric problems. They belong to a sub branch of mathematics known as combinatorics.
The mathematicians grounded their method in the concept of Catalan numbers, a series utilized for counting the various methods to triangulate polygons. These numbers were initially outlined by Mongolian mathematician Mingantu circa 1730 and later rediscovered by Swiss mathematician Leonhard Euler in 1751. Recognizing an opportunity, Wildberger and Rubine explored advanced versions of these numbers as potential solutions for more complex polynomial equations. They named this expanded idea “the Geode.”
The Geode offers multiple possible uses for upcoming studies, particularly within the realms of computer science and graphic design. "This represents a significant overhaul of an essential section in algebra," stated Wildberger.
Like this article? For more stories like this, follow us on MSN by clicking the +Follow button at the top of this page.
0 Response to "'Mathematicians Unveil Revolutionary Algebraic Method for Solving Complex Equations'"
Post a Comment